R
ggplot2
ggplot basics
# Start with:
ggplot(data, aes(X,Y, fill = if_needed)) +
# Hist:
geom_hist(bins, aes(y = after_stat(density))) # for denmsity if needed (Prob. distr.)
# Boxplot:
geom_boxplot()
# StackedCol:
geom_bar() OR geom_bar(position = "fill") # for 100%
# Scatter:
geom_point() + stat_smooth(method= lm) # if needed!
## Additionals:
### Density (PMF/PDF) to a histogram:
geom_hist() + stat_function(fun = dnorm/d..., args(list({ami a d... functionbe kell})), color='', linewidth=num )
### Optical:
labs(X,Y, fill = , title=) # Labels, titles
theme(axis.text.x=element.blank, ...) # ThemeDistribution plot
mu = mean(Tesla$TESLA)
sigma = sd(Tesla$TESLA)
ggplot(Tesla, aes(x=TESLA)) +
geom_histogram(aes(y = after_stat(density))) +
stat_function(
fun = dnorm,
args = list(mean = mu, sd = sigma),
col = 'red')Regular lm plot
ggplot(data = BP_Flats, aes(x = Area_m2, y = Price_MillionHUF)) +
geom_point() +
stat_smooth(method=lm)# layer fitting a trend line || without lm for non-linear fittingInteractions plot
ggplot(data = BP_Flats, aes(x = Area_m2, y = Price_MillionHUF, color = IsBuda)) +
geom_point() +
stat_smooth(method=lm)Box plot
ggplot(data = BP_Flats, aes(y = Price_MillionHUF, fill = District)) +
geom_boxplot() +
labs(y = "Price in million HUF", fill = "District", title = "Distribution of Apartment Prices by Districts") +
theme(axis.text.x = element_blank(),
axis.ticks.x = element_blank(),
axis.text.y = element_text(size = 16),# font size of the 'y' axis
plot.title = element_text(size = 20, face = "bold", color = "darkgreen"))# font size, font style (bold) and font color for the text in the plot titleboxplot(BP_Flats$Price_MillionHUF ~ BP_Flats$District) # after the tilde symbol, we provide the factor by which we want the plot to be split
100% stacked column plot
ggplot(data = BP_Flats, aes(x = IsBuda, fill = IsSouth)) +
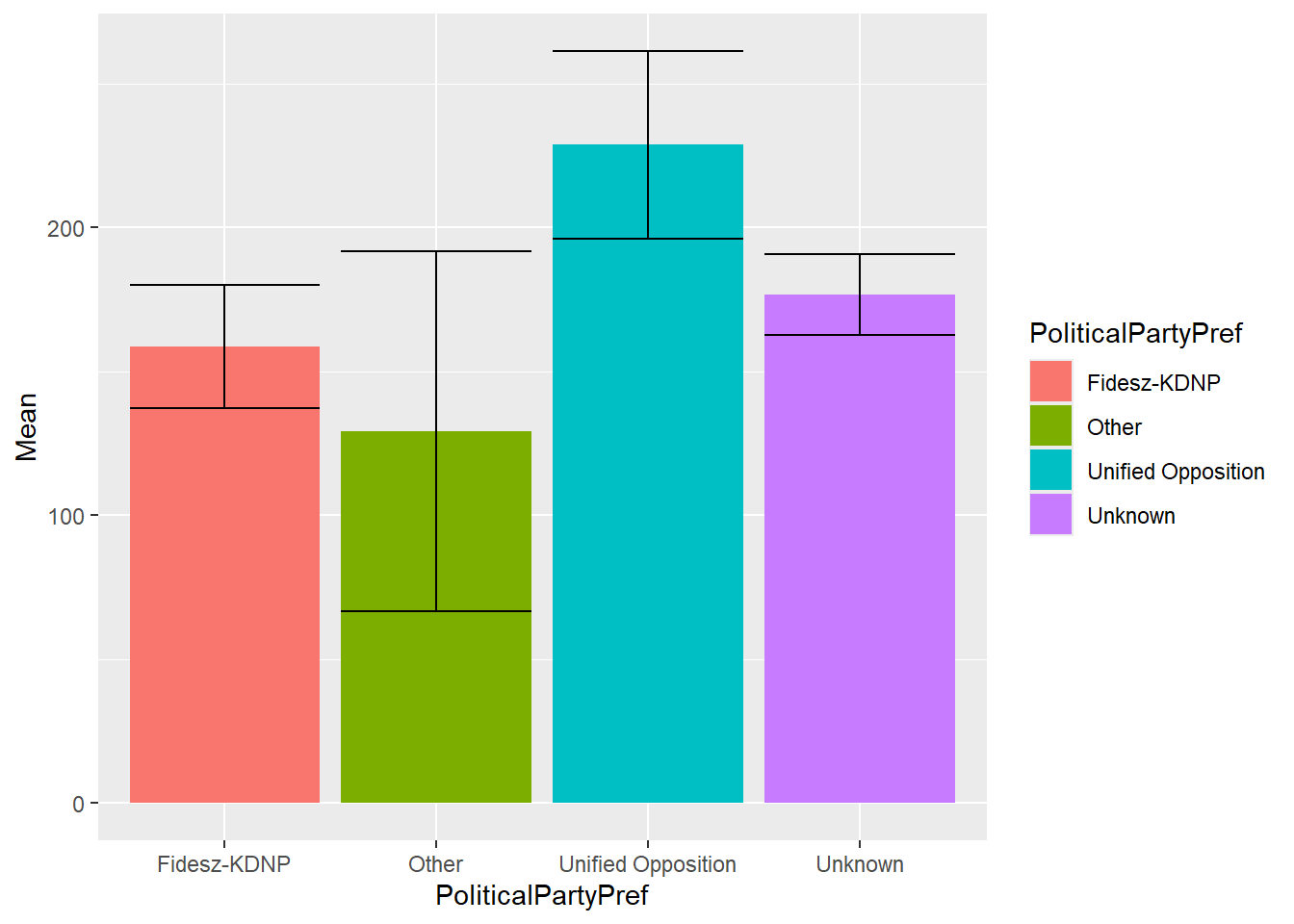
geom_bar(position = "fill")Column plot with error bars for group means
conf_int_df <- groupwiseMean(NetUsePerDay_Minutes ~ PoliticalPartyPref, data = ESS, conf = 0.99,
na.rm = TRUE, digits = 4)
ggplot(conf_int_df, aes(x = PoliticalPartyPref, y=Mean, fill = PoliticalPartyPref)) +
geom_bar(stat = "identity") +
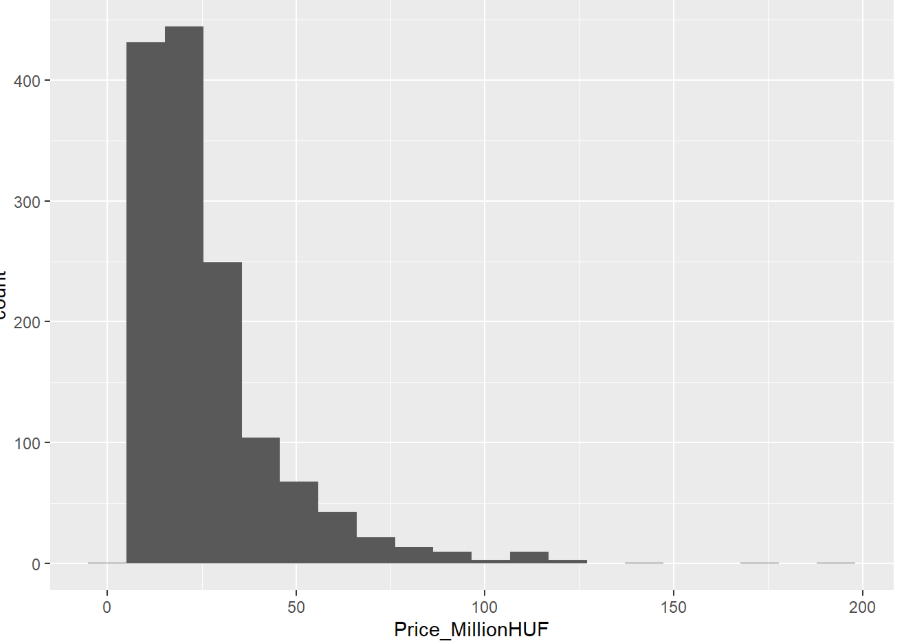
geom_errorbar(aes(ymin=Trad.lower, ymax=Trad.upper))Histogram
ggplot(data = BP_Flats, aes(x = Price_MillionHUF)) +
geom_histogram(bins = 20)Labels
p1 <-ggplot(mtcars2) +geom_point(aes(x = wt, y = mpg, colour = gear)) +labs( title = "Fuel economy declines as weight increases", subtitle = "(1973-74)", caption = "Data from the 1974 Motor Trend US magazine.", tag = "Figure 1", x = "Weight (1000 lbs)", y = "Fuel economy (mpg)", colour = "Gears" )R Csomagok
| Függvény | Syntaxis | Csomag | H0 | Teszt |
|---|---|---|---|---|
by(BP_Flats[,c("Price_MillionHUF", "Area_m2", "IsSouth")], BP_Flats$IsBuda, summary) | ||||
| Gini | #Step 1: Package Installationinstall.packages("DescTools")#Step 2: Defining vector of incomesx <- c(50, 50, 70, 70, 70, 90, 150, 150, 150, 150)#Step 3: Calculate Gini coefficientGini(x, unbiased=FALSE) | DescTools | 0: teljes egyenlőség 1: teljes monopólium | |
| hhi | a <- c(1,2,3,4) # arbitrary firm id# market share of each firm (should total 100% of market share)# create data frame# calc | hhi | min: 1/n | |
| Spearman cor | cor.test(x, y, method = "spearm", alternative = "g") | stats | ||
| pairs.panels | pairs.panels(df) | psych | ||
| fitdist, denscomp | fit_norm <- fitdist(Surv$SurvMonth, "norm", method = "mle")summary(fit_norm)denscomp(list(fit_expon, fit_norm)) | fitdistrplus | ||
| corrplot | corrplot(KorrelMatrix, method="color")corrplot(KorrelMatrix, method="number") | corrplot | ||
| Gyakoriság, rel.gyak. | prop.table, table | stats | ||
| describe | describe(BP_Flats) | psych | ||
| groupwiseMean | groupwiseMean(NetUsePerDay_Minutes ~ PoliticalPartyPref, data = ESS, conf = 0.99, na.rm = TRUE, digits = 4) | rcompanion |
Hipotézis tesztek (vizsgálatok)
Egy minta
Population Mean t-test
# CHECK!!!
1) n >= 50 --> :)
2) n < 50 --> data ~ NormalDistr()
t.test(df$column, mu = mu_0, alternative = "less/greater/two.sided")
# mu_0: becsült mu
# H1 eldöntése, side:
# 1) H0: mu = mu_0 H1: mu != mu_0 --> two.sided
# 2) H0T: mu >= mu0 H1: mu < mu0 --> left sided
# 3) H0T: mu <= mu0 H1: mu > mu0 --> right sidedPopulation Proportion (z-test)
# CHECK!!!
c(n*P_0 >10, n*(1-P_0) > 10
auto:
prop.test(x, n, p = p_e, alternative=...)
# p_e --> expected Proportion
manualis teszt...
1) test stat: (P-P0)/(sqrt((P0*(1-P0))/n))
2) p-value: pnorm(test_stat)
3) two.sided: 2*pnorm() right: 1- pnorm() left: pnorm()Population St.Dev. (ChiSq-test)
# CHECK!!!
data ~ Normal
manualis teszt...
1) test stat: (n-1)*s2/sigma^2
2) p-value --> two.sided: 2*pchisq() right: 1- pchisq() left: pchisq()Ket minta
Welch t-test Population Mean
# CHECK!!!
1) n >= 50 --> :)
2) n < 50 --> data ~ NormalDistr()
t.test(numerikus ~ nominalis, data, mu = delta_0, alternative = "less/greater/two.sided")
# delta_0: kulonbsege a ket becsult csoportnakPopulation Proportion z-test
# CHECK!!!
c(k1>10, k2>10, n1-k1>10, n2-k2>10)
manualis teszt:
test_stat <- ((P1-P2)-epsilon0)/sqrt(((P1*(1-P1))/n1)+((P2*(1-P2))/n2))
# epsilon0 ~ delta0
# / sqrt(...): Unified SE (standard error)Nem paraméteres tesztek
Feltetel: 10≥f_ij
- Reprezentativitás tesztje
chisq.test(table(Catbus$Gender), p=c(0.6, 0.4)) # p: elmeleti eloszlas, pl 40% no- Normalitás tesztje
auto:
shapiro.test(Catbus$Steps)
ks.test(Catbus$Steps, 'pnorm') # ebben nem lehetnek ismetlodo ertekek
tseries::jarque.bera.test(Catbus$Steps)
#-------------------------------------------------------------------------------------------------
manualis:
theor_quantiles <- qnorm(c(0,0.2, 0.4, 0.6, 0.8,1), mean=mean(Catbus$Steps), sd=sd(Catbus$Steps))
obs_freq <- table(cut(Catbus$Steps, breaks=theor_quantiles))
chisq.test(obs_freq) # p-value=11% => fail to reject H0 => it follows normal distribution- Homogenitás tesztje
sfh <- readxl::read_excel('StackOverflowHungary2020.xlsx')
sfh
sfh$isWin <- sfh$OpSys == 'Windows'
(crosstab <- table(sfh[,c('JobSat', 'isWin')]))
hom_test <- chisq.test(crosstab) # p-value=20% => nem utasithato el a H0 => a ket csoport homogen
hom_test$expected - hom_test$observedKetvaltozos statisztikai relationship xd
- X és Y is kategorikus ⇒ asszociáció vizsgálata ⇒ homogeneitás teszt
- X kategorikus és Y numerikus ⇒ ANOVA (hasonló a PS mintavételhez)
- X és Y is numerikus ⇒ korreláció / regresszió
Mindegyiknek két része van:
- erősség / hatásnagyság
- szignifikancia
Asszociáció (kat ~ kat)
Vizualizáció: 100% stacked oszlopdiagram → excel!
# 100% stacked oszlopdiagram, de bonyolult rátenni %-okat
ggplot(csok, aes(settlement, fill=CSOK3children)) +
geom_bar(position = "fill")Százalékok
crosstab <- table(csok[,c("settlement", "CSOK3children")])
# százalékos eloszlás
round(prop.table(crosstab)*100, 1)
# vízszintesen eloszlás (csoportokon belül)
round(prop.table(crosstab, 1)*100, 1)
Hatásnagyság: Cramér-féle V együttható
- interpretáció: 0.3, 0.7 — gyenge, közepes, erős
- R-ben:
rcompanion::cramerV(crosstab) #0.078 => gyenge kapcsolat questionr::cramer.v(crosstab) # manuálisan sqrt(test_of_indep$statistic/(nrow(CSOK)*(2-1)))
Szignifikancia: Khi-négyzet próba, függetlenségvizsgálat
- feltétel: minden elméleti csoportban min 5 tag
chisq_test_result$expected > 5
- H0: nincs szignifikáns kapcsolat a változók között a sokaságban
- R
chisq.test(crosstab)ANOVA (num ~ kat)
Két része van:
- erősség - mennyire befolyásolja?
- szignifikancia - populáción kívül is megfigyelhető?
Vizualizacio: csoportositott boxplot
boxplot(price ~ CSOK3children, data=csok)Erősség tesztelése
- hatásnagyság/hatásmérték (variance ratio)
- ANOVA esetében: eta-négyzet
- interpretáció: 0.1, 0.5 hasonlóan az R-négyzethez (gyenge, közepes, erős) és százalékként.
- Az Y változó varianciájának 12.3%-át magyarázza az X változó a megfigyelt mintában.
- R-ben:
# ANOVA boxplot(price ~ CSOK3children, data=csok) anova_model <- aov(price~CSOK3children, data=csok) lsr::etaSquared(anova_model) # 12.3% => közepes erősségű kapcsolat
Szignifikancia tesztelése (F-teszt)
- H0: az eta-négyzet a sokaságban 0 (nem szignifikáns az összefüggés), H1: eta > 0
- feltétel: n>100 minden csoportban
# szignifikancia
table(csok$CSOK3children) # all > 100
# H0: eta=0, H1: eta>0
oneway.test(price ~ CSOK3children, data=csok)
# p-value < 0.1% => H0 elutasitva, szignifikans osszefuggesEredmény: szignifikáns, de gyenge kapcsolat (a kettő külön van!!)
Logisztikus regresszio
Step-by-Step:
- Adat elokeszites
- Y valtozo Binaris?
- Faktorizalas
- Referencia szint
- Modellepites
- Model tisztitas
- Nem szignifikans valtozok
- VIF
- Interpretacio
exp(coef(model))
- Modell josaga
- Globális teszt anova
- McFadden R^2
- Kallifikacios tabla
- ROC és Cut off ha kell
Side note: Multinomiálisnál mindig a referencia kategoriahoz kepest ertelmezendo (mennyivel valoszinubb hogy elégedett mintsem hogy nagyon elégedetlen)
Logit Transzformácio
logisztikus_bovebb <- glm(Survived ~ Age + Fare + Sex, family = binomial(link='logit'), data = titanic) # family = binomial -> eredmeny binaris (0 vagy 1)
summary(logisztikus)
exp(logisztikus$coefficients) # βAge=0.98 -> Ha kor +1 akkor tuleles 2% csokken az odds
library(car)
vif(logisztikus_bovebb) # LEHET RAJTA VIF-et futtatni- Modellek összehasonlitasa AIC() és BIC()
titanic$Probability_Bovebb <- predict(logisztikus_bovebb, newdata = titanic, type = "response") # type=response P(y=1) valoszinuseg
titanic$y_kalap <- 0 # alapból azt mondom mindenki meghal
titanic$y_kalap[titanic$Probability_Bovebb > 0.5] <- 1 # akinek tulelese nagyobb mint 50% azt jelolje tuleltnek
table(titanic[,c("y_kalap", "Survived")])- accuracy= jok/osszes
- precision(1) = jol predictelt / osszes pl. tuleltre
- recall(1) jol predictelt /valojaban pl. tulelt
Ritka események
csod$BecsultCsod <- 0 # kezdetben mindenki fizetőképes marad
csod$BecsultCsod[csod$CsodVsz > 0.054] <- 1 # akinek 5.4%-nál magasabb a csődvalószínűsége, azt csődösnekROC Gorbe
table(csod[,c("csod", "BecsultCsod")]) # klasszifikációs matrix- szenzitivitas (TPR) = jol becsult csod / osszes becsult csod
- specificitas = jol becsult nem csod / osszes becsult nem csod
- 1 - specificitas = FPR
library(pROC)
ROC_adatok <- roc(csod$csod, csod$CsodVsz)
plot(ROC_adatok)
ROC_adatok$auc # area under curve
legjobb_cutoff <- coords(ROC_adatok, "best", ret = "threshold", best.method = "closest.topleft")
legjobb_cutoff
csod$BecsultCsod <- 0 # kezdetben mindenki fizetőképes marad
csod$BecsultCsod[csod$CsodVsz > legjobb_cutoff[1,1]] <- 1
table(csod[,c("csod", "BecsultCsod")])Asszimetrikus dontes
pl.
- helyes dontesnel (True Negative) felismerjuk jo ugyfelet -> nyerunk 1 egységet
- tévedésnél (false Negative) jonak hiszunk rossz ugyfelet -> bukunk 10 egyseget
- Alap hasznosság pl. 1TN + 10 FN
hasznossag <- function(x) {
csod$BecsultCsod <- 0
csod$BecsultCsod[csod$CsodVsz > x] <- 1
klassz_matrix <- table(csod[,c("csod", "BecsultCsod")])
hasznossag_ertek <- 1*klassz_matrix[1,1] - 10*klassz_matrix[2,1]
return(hasznossag_ertek)
}
eredmeny <- optimize(hasznossag, c(0,1), maximum = TRUE)
eredmeny # maximum = optimalis cutoff , objective = Maximalis hasznosságR^2 nincs itt, ha nagyon akarunk egy mutatot mint OLSnel R negyzet:
library(DescTools)
PseudoR2(csod_logit, "McFadden")- Mennyivel lett jobb a modellünk a véletlen tippelésnél (null modellnél)."
- Egy 0.2-0.4 közötti érték már kiválónak számít!
Hipotezis teszt
Globális illeszkedés test
H0: a modellunk haszontalan, nem magyaraz
logit_nullmodell <- glm(csod ~ 1, family = binomial (link = "logit"), data = csod)
# 1-gyel jelezzük, hogy nem akarunk magyarázóváltozókat a modellben!
anova(logit_nullmodell, csod_logit)
p_ertek <- 1 - pchisq(Deviance, Df) # Deviance es Df az anova eredmenyenel van 2. sorvagy Hosmer-Lemeshow Teszt → H0: jol illeszkedik
library(ResourceSelection)
hoslem.test(titanic$Survived, fitted(logisztikus_bovebb))Multinomiális Logisztikus Regresszió
Ha eredményváltozó > 2 (levels(ProgData$JobSat))
ProgData$JobSat <- relevel(ProgData$JobSat, ref = "Very dissatisfied")
library(nnet)
multi_logit <- multinom(JobSat ~ Age + YearsCodePro + MonthlyHuf, data = ProgData)
summary(multi_logit)
exp(coef(multi_logit))library(lmtest)
lrtest(multi_logit, "Age") # p-érték H0: nem szignifikansÁltalános ajanlas: n>parameters*5 length(coef(multi_logit))
Össze lehet vonni pl neither satisfied a slightly dissatisfied
lrtestek alapjan maradjanak szignifikansak → uj model
Összehasonlitas AIC() BIC()
ProgData$JobSatPredicted <- predict(multi_logit_szuk, newdata = ProgData, type = "class")
klassz_matrix <- table(ProgData[,c("JobSat", "JobSatPredicted")])
round((sum(diag(klassz_matrix))/sum(klassz_matrix))*100,2)Pszeudo R^2
library(DescTools)
PseudoR2(multi_logit_szuk, "McFadden")- Mennyivel lett jobb a modellünk a véletlen tippelésnél (null modellnél).
- Egy 0.2-0.4 közötti érték már kiválónak számít! (pl. 0.3 modell 30% javitotta az elorejelzes minoseget ahhoz kepest ha tobbsegi atlaggal random tippeltunk volna)
Lineáris regresszió
álkorreláció = spurious regression
Standard regressziós modell feltételek (Gauss-Markov kondíciók):
- n > 100
- strong exogeneity (mean(residuals) = 0)
- LINEAR form
- no exact multicoll
- no autocorrelation
- homoscedasticity (NOT heterosked.)
lmtest::bptest(model)
skedastic::white(model)
Osszes package ami kellhet
skedastic lmtest car margins lsr tseriesAlap cuccok
csok_model <- lm(log(price)~log(area)+settlement+CSOK3children+type, data=csok)
summary(csok_model)
lmtest::resettest(csok_model) # RESET, specifikációt nézi (H0: well specified)
anova(model_restricted, model_unrestricted) # Wald test, Restricted és Unrestr. modellek (kell-e az a plusz) variable (H0: nem szignif. a plusz variable, restricted nyert)
skedastic::white(csok_model) # White test, heterosked (H0: homosked.)
--> lmtest::coeftest(model, vcov=car::hccm(model))
lmtest::bptest(model, studentize=T)
car::vif(csok_model) # multikollinearitas (5, 10(erősen) felett baj van)
--> full_pca <- prcomp(data[,],center=TRUE, scale=TRUE) --> summary() # captured Var >1 az jo
# dy/dx - marginal effect
margins::dydx(csok, csok_model, 'settlement') #
head(dydx(household[household$Muni=="City",], int_model, "IncTFt" ))
confint(csok_model) # egyutthatok konfidenciaintervalluma
lmtest::coeftest(model) # partial t-testek + együtthatók
# log-log model
lm...
estim <- predict(loglog, newdata=df[,])
estim <- exp(estim)
loglog$coefficients[i] * estim / df$var[i] # loglog$coefficients[i] --> partia lelasticity (%!)
# interakcio
ggplot(csok, aes(area, price, col=settlement)) + geom_point() + geom_smooth(method=lm)
csok_model2 <- lm(log(price)~log(area)+settlement+CSOK3children+type + area*settlement, data=csok)
summary(csok_model2)